
В какой-то момент математики
Например, найти верный корень в уравнении снизу.
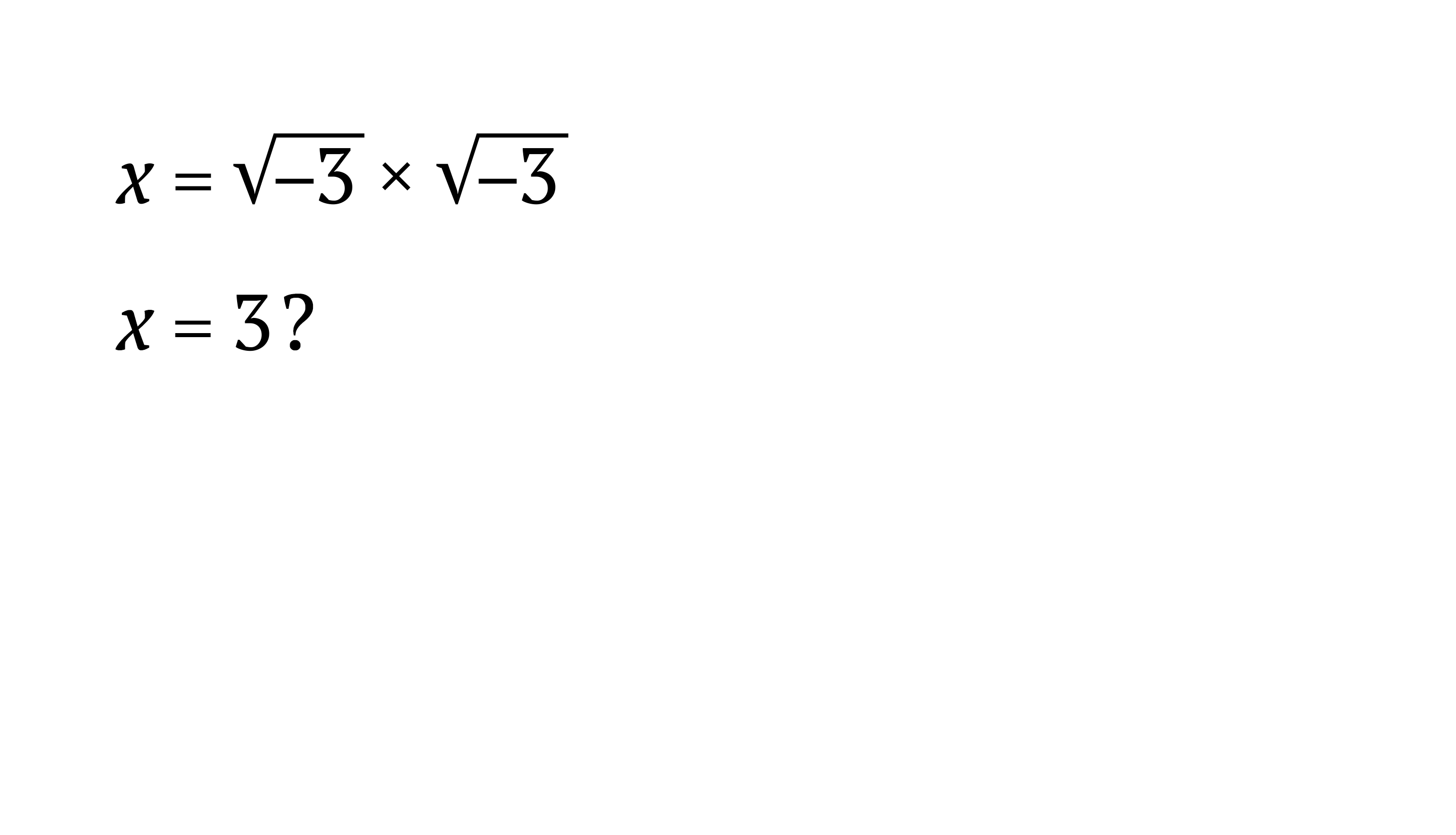
Тогда они придумали несуществующее число, которым ничего нельзя посчитать, но которое помогло им решить уравнение. Это число i, равное корню из минус одного. Совершенно абстрактная, но полезная ерунда.
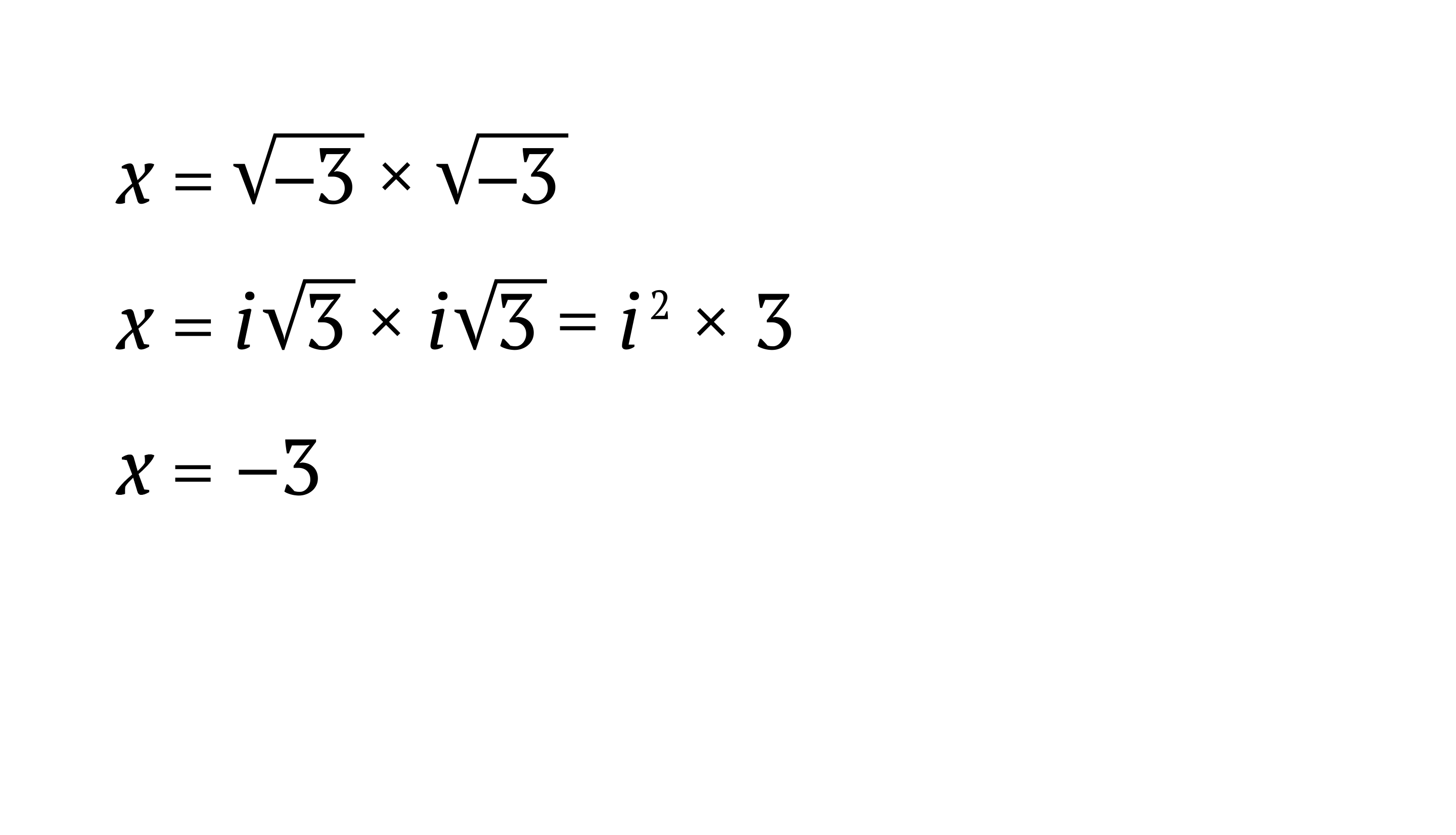
Появились комплексные числа, у которых кроме нормальной, понятной части, появилась еще непонятная, где есть это i. Понятная часть называется вещественной, а непонятная — мнимой.

Раз уж комплексные числа состоят из двух частей (вещественной и мнимой) и координаты пикселей на экране тоже состоят из двух частей (сколько до него по горизонтали и сколько по вертикали), то можно нарисовать на экране карту комплексных чисел. Или, по-другому, комплексную плоскость.
На этой комплексной плоскости можно отметить любое комплексное число, например –1,3 + 0,8i
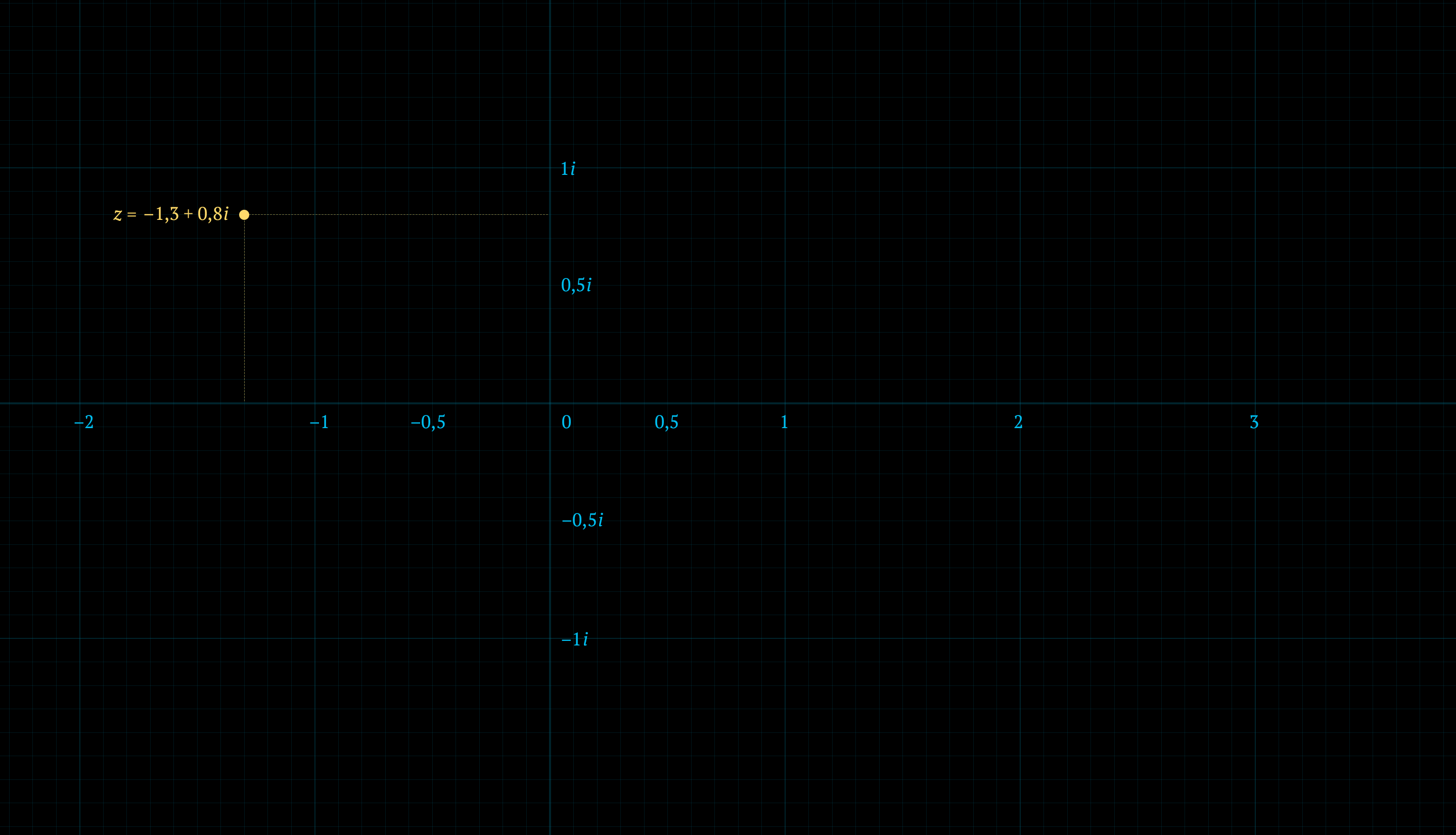
Множество Мандельброта — это группа комплексных чисел, которые проходят определенный фейс-контроль.
Правила такие: берем ноль, умножаем его на самого себя и прибавляем к комплексному числу, которое хотим проверить. Затем полученный результат умножаем на самого себя и опять прибавляем к нашему числу. Затем снова и снова, опять и опять. И так до бесконечности. С каждым подходом получается новое комплексное число, которое либо уходит все дальше и дальше от центра, либо нет.
Если оно сваливает в бесконечность — значит первоначальное число не прошло фейс-контроль. Если остаётся — добро пожаловать в множество Мандельброта.
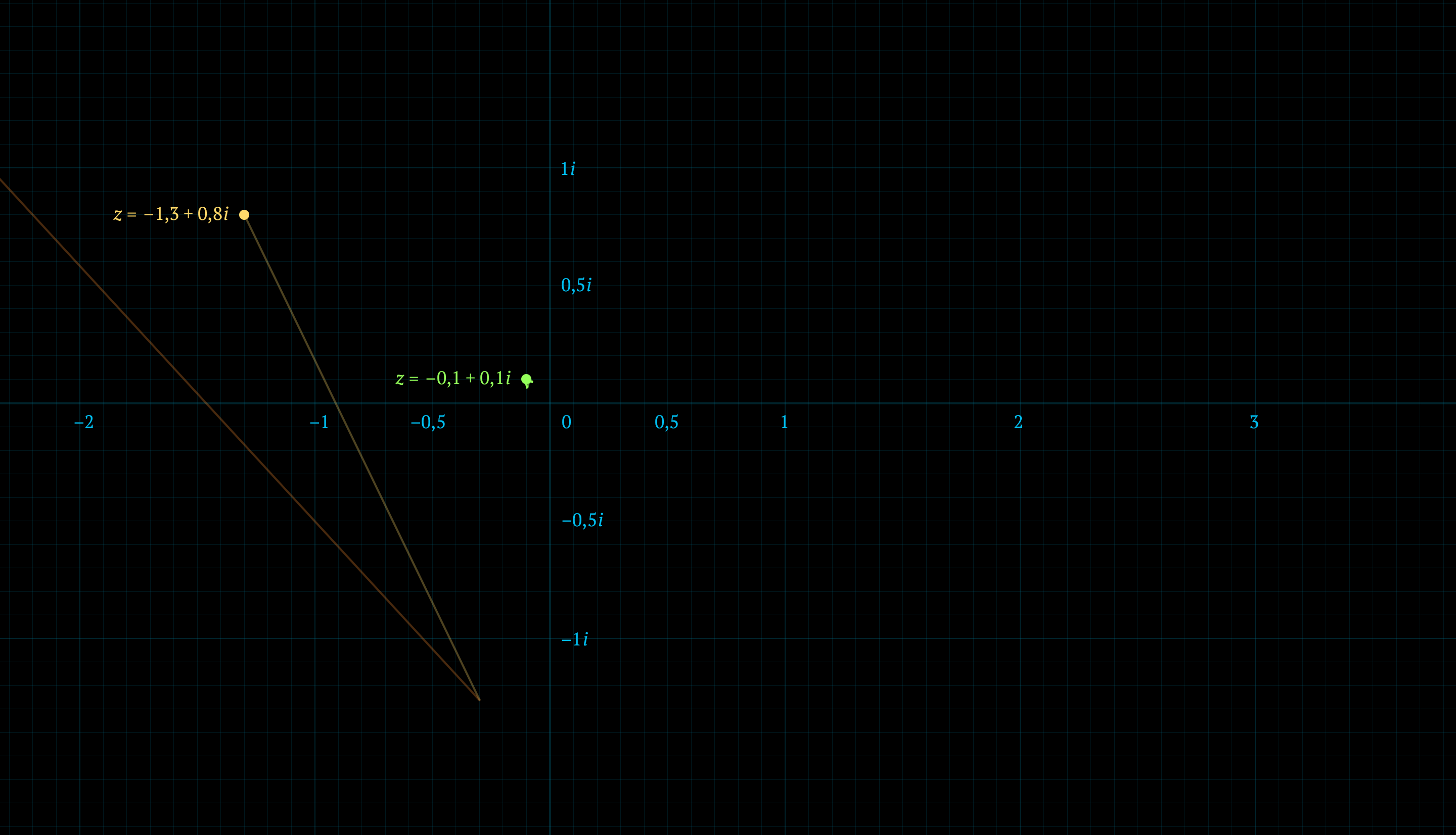
Как можно увидеть, число –1,3 + 0,8i со второго подхода отправилось в закат, а вот -0,1 + 0,1i никуда не делось, сколько мы его ни дёргали.
Проверим каждый пиксель на экране:
Получается что-то, похожее на жопу (по-научному «кардиола»). То, что закрашено белым цветом, входит в множество Мандельброта. Всё остальное — нет.

Если приблизить картинку, то мы увидим всё новые и новые детали на границах жопы. Снизу — часть предыдущей картинки. Она увеличена в 13 раз. Фишка в том, что плоскость можно приближать сколько угодно, всегда будет проявляться что-то новое, хотя и похожее на предыдущее. Такая штука называется фракталом.

Какая-то область фрактала, увеличенная в 210 000 раз. Видны только несколько маленьких жоп. Можно приближать и дальше, но всё равно мы получим круги и новые жопы. Не очень впечатляет.

Вспомним, что картинка рисуется так: мы проверяем каждое комплексное число много-много раз, пока не поймем, проходит ли оно фейс-контроль. Дополним картинку: чем быстрее число уходит в бесконечность, тем темнее цвет. Мгновенно улетело в пустоту? Почти черный. Едва-едва ползёт? Почти белый. Вот что получается:
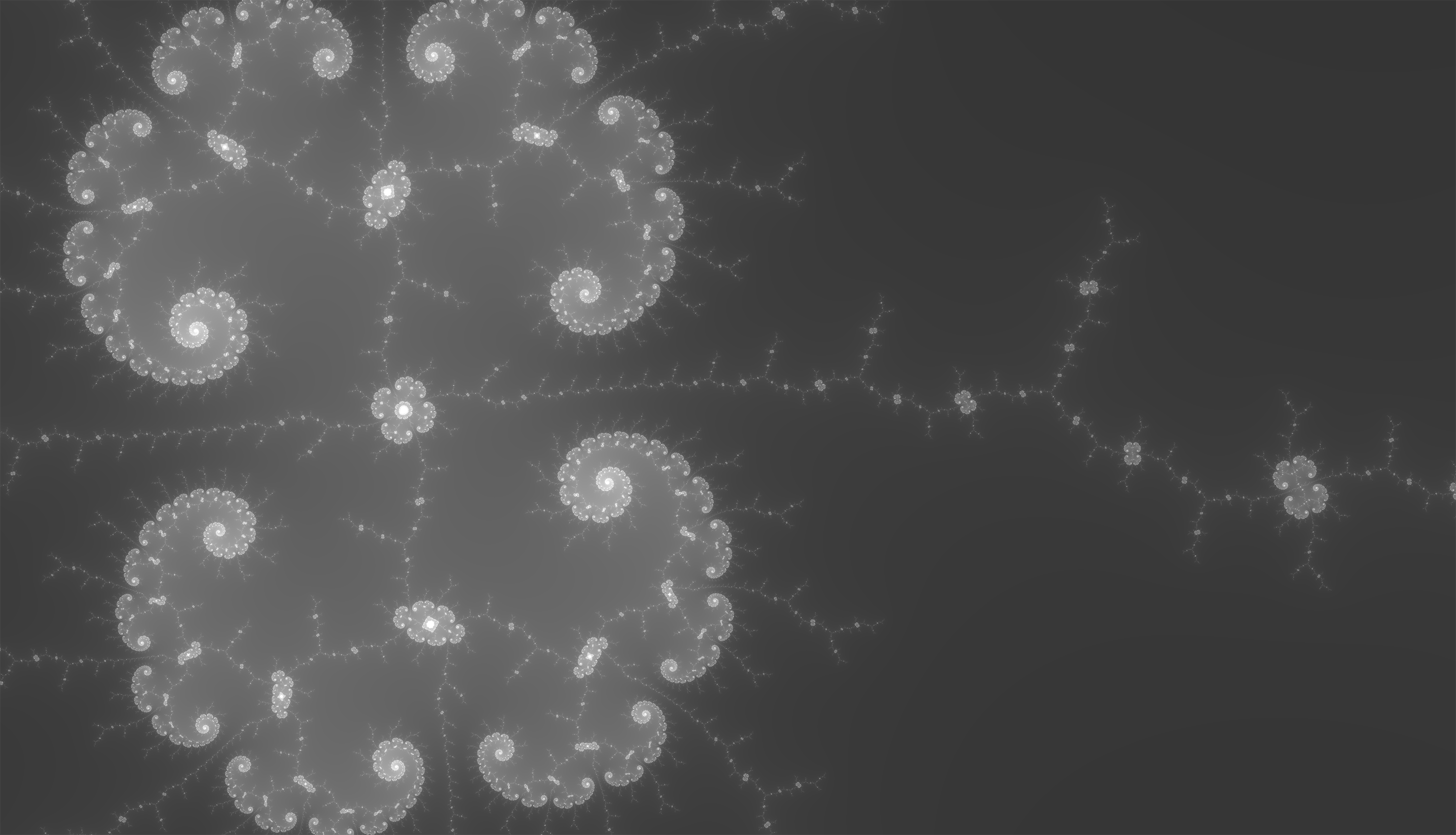
Офигеть, правда?
Почти все точки на экране не входят в множество Мандельброта, но все сваливают от него с разной скоростью.
Можно раскрасить картинку не чёрным и белым, а вот так:

Есть еще один крутой способ раскрасить картинку. Можно взять один набор цветов и залить не всё сразу, а раскрасить только 50% самых быстросваливающих. От оставшихся взять снова 50% и раскрасить. Потом еще 50% и так далее. Вот что получится, если взять только черный и белый цвета:

Рисунок стал контрастнее и интереснее в деталях.
Осталось добавить цвет.
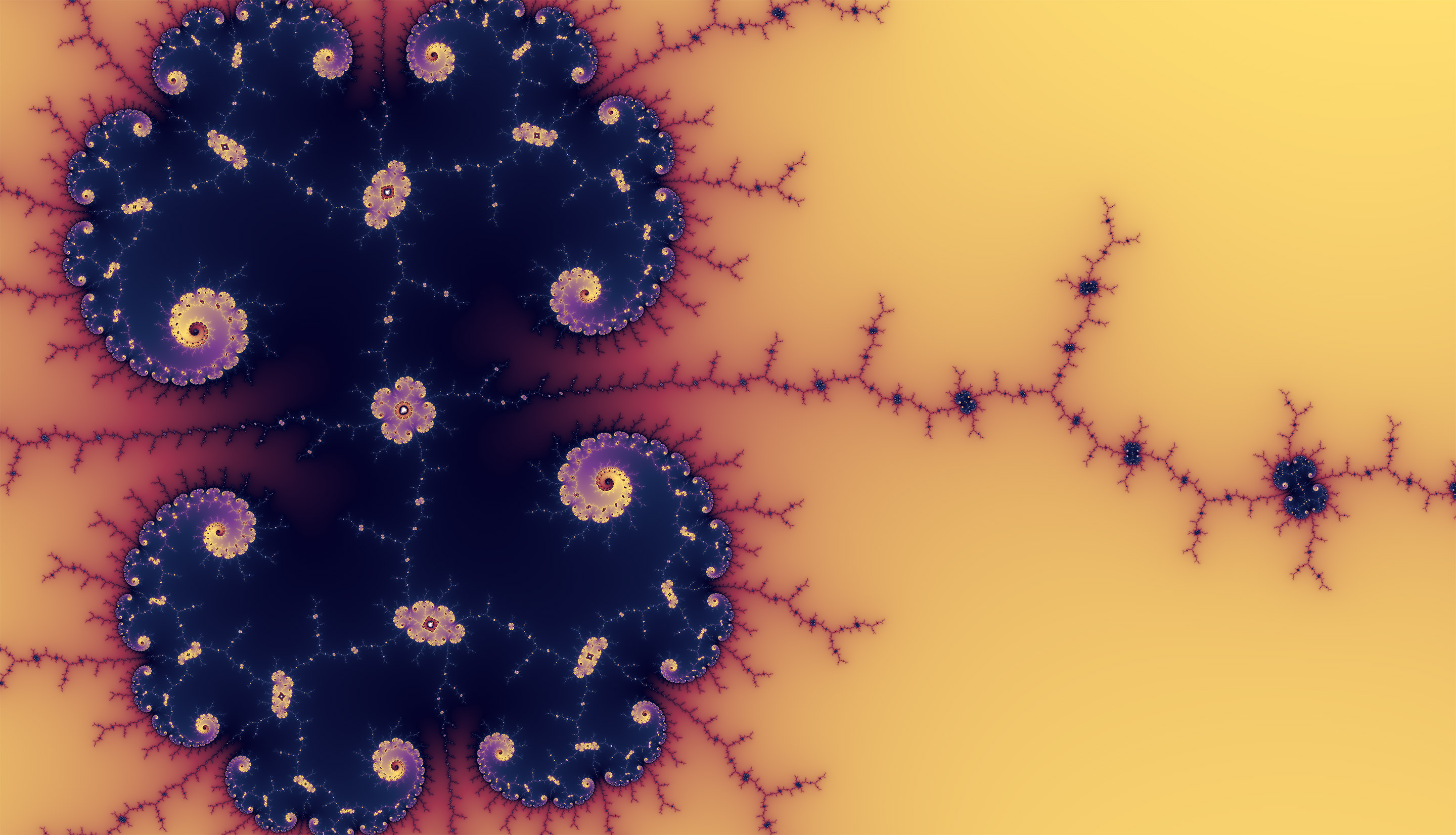
Чёрная медуза.

Циклон.
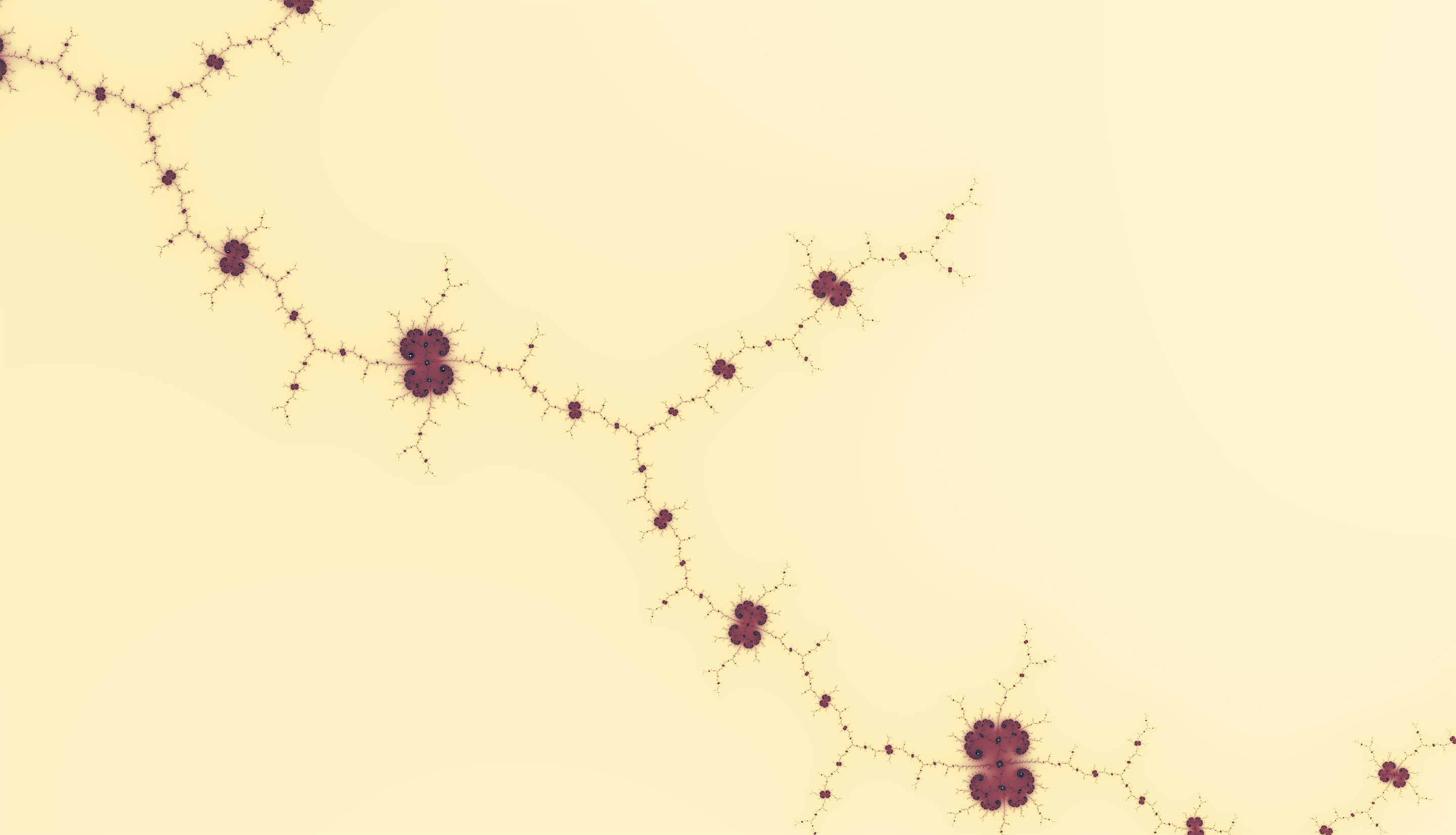
Медузы выползают из трещины.
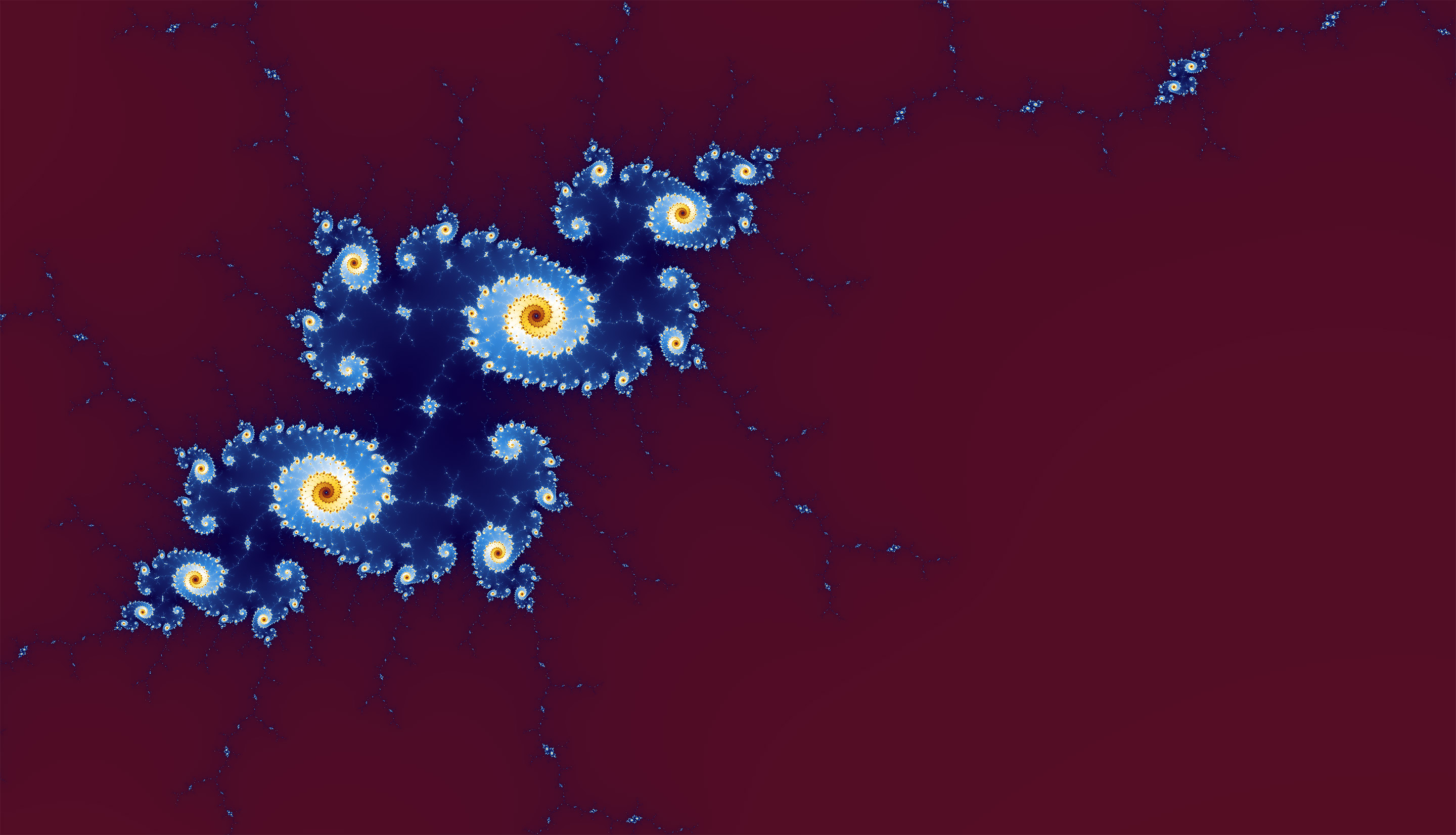
Остров Жюлиа. Это официальное название. Филиал множества Жюлиа во множестве Мандельброта.
В центре острова бесконечное число оцеплений из циклонов охраняет короля жоп.

У больших циклонов в оцеплении есть свой шарик на ниточке.

Слои охраны около жала короля жоп. За каждым оцеплением своя атмосфера, которая просачивается между циклонами.

Жопа без охраны поросла двузубчатой электрической плесенью.
Хищная жопа-убийца раскинула ядовитые лапы в ожидании жертвы.
Долина вилок.
Долина полувилок.

Долина супервилок.

Волли.

Луна.

Солнце.

Тайфун.
Если чуть-чуть поменять правила


Флот горит.

Падающий собор.

Небоскрёбы.

Вода под килем флагмана.

Океан.
Все картинки, кроме самых первых, сгенерированы в браузере.
![]() 2016 Sunandstuff
2016 Sunandstuff
[email protected]
Спасибо Пьеру Фату, Бенуа Мандельброту и Отто Рёслеру за алгоритмы; Википедии, Стигену Ларсену и сайту Микрософта (там реально есть раздел про визуализацию множества) за понимание этих алгоритмов; Линасу Вептасу за алгоритм вычисления скорости расхождения рядов (я все равно не врубился, как это работает, потому что плохо учил в школе логарифмы); а также фоточке раскалённой железяки из интернета за палитру «Forest fire».